ACM Coffee Break Puzzle Number 1: Logic Puzzle
You have three boxes, one containing red balls, one containing blue balls, and one containing a mixture of both red and blue balls. Each box is labeled, but all labels are incorrect. You are allowed to open just one box and take out one ball. By looking at the ball, how can you determine the correct labels for all three boxes?

ACM Coffee Break Puzzle Number 2
The program on the next slide aims to find the first 10 prime numbers and print them. However, there is a bug in the program and it does not work.

Identify the bug in the program and fix it.

ACM Coffee Break Puzzle Number 3
You are at a magical lake guarded by three mystical creatures: a dragon, a mermaid, and a unicorn. Each creature always tells the truth or always lies. The dragon says, “The mermaid always lies.” The mermaid says, “The unicorn always tells the truth.” The unicorn says, “I am the only one here who tells the truth.” If only one creature tells the truth, which creature is it?

ACM Coffee Break Puzzle Number 4
You have a four-minute hourglass and a seven-minute hourglass. How do you measure nine minutes?

ACM Coffee Break Puzzle Number 5
Four people need to cross a bridge at night and it’s too dark to cross without a flashlight. Only one flashlight is available. The bridge can support only two people at a time. Each person takes a different amount of time to cross: 1 min, 2 min, 7 min, and 10 min. What is the shortest possible time for all four people to cross the bridge?

ACM Coffee Break Puzzle Number 6
A room in an old house contains 3 light bulbs, each connected to 1 of 3 switches outside the room. The door to the room is closed. You can operate the switches freely, but you can only open the door once, and you can’t change the switches after opening it. All bulbs work. Identify which switch controls each bulb.

ACM Coffee Break Puzzle Number 7
A circular birthday cake has to be divided into 8 equal pieces within 3 cuts. How can you do it?

ACM Coffee Break Puzzle Number 8
You have $15. You go to a chocolate shop and find that the price per chocolate is $1. The shopkeeper tells you that you can also get a chocolate in exchange for 3 wrappers. What is the maximum number of chocolates that you can get?

ACM Coffee Break Puzzle Number 9
You stand before two doors: one leads to heaven, the other to hell. Two guards stand watch; one always tells the truth, the other always lies, but you don’t know who is who. You can ask one question to one guard to find the door to heaven. What do you ask?

ACM Coffee Break Puzzle Number 10: Tomato Soup
You have a bowl of tomato soup. You have one other empty bowl of a different size and shape. You have to give the soup to two children. How would you divide the soup into two bowls so that both of them are satisfied that they have got an equal share of soup?

ACM Coffee Break Puzzle Number 11: Gold Bar
You have hired someone to work for you for seven days, and you have a gold bar to pay him. You must give him a piece of gold every day. What is the least number of cuts you can make to the gold bar such that you can pay this person 1/7th of it each day?

ACM Coffee Break Puzzle Number 12: Tennis
Mark and Lisa decided to play tennis against each other. They bet $1 on each game they played. Mark won three games and Lisa won $6. How many games did they play?

ACM Coffee Break Puzzle Number 13: Math
How many times can you subtract the number 5 from 35?

ACM Coffee Break Puzzle Number 14: Thanksgiving
At Thanksgiving dinner, five family members, Anna, Ben, Clara, David, and Emily, each brought a different dish. The dishes were: turkey, stuffing cranberry sauce, mashed potatoes, and pumpkin pie. However, nobody remembers who brought what. Using the clues below, can you figure out who brough each dish?
Anna is allergic to cranberries. Ben brought something savory, not sweet. Clara dislikes baking. David brought the dish traditionally served as the main course. Emily brought a savory dish that pairs well with turkey but is not mashed potatoes.

ACM Coffee Break Puzzle Number 15: Lost Dog
A man stands on one side of a river, his dog on the other. The man calls his dog, who immediately crosses the river without getting wet and without using a bridge or a boat. How did the dog do it?

ACM Coffee Break Puzzle Number 16: Triangles

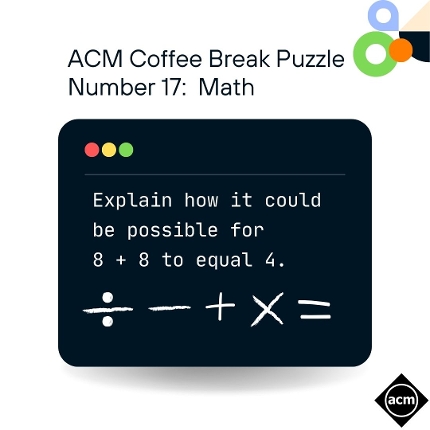
ACM Coffee Break Puzzle Number 17: Math
Explain how it can be possible for 8 + 8 to equal 4.
ACM Coffee Break Puzzle Number 18: Tires
Which tire doesn't move when a car turns right?

ACM Coffee Break Puzzle Number 19: Brothers
One brother says of his younger brother: "two years ago, I was three times as old as my brother was. In three years time, I will be twice as old as my brother." How old are they each now?

ACM Coffee Break Puzzle Number 20: What am I?
I have keys, but open no locks. I have space, but no room. You can enter, but you can't go outside.
What am I?

ACM Coffee Break Puzzle Number 21: Apples
A farmer tells his three children: "I have a number of apples in a basket. If I divide them equally among you, one apple remains. If I divide them among two of you, one apple still remains. But if I take just one apple away, the remaining apples can be evenly split among all three of you. How many apples are in the basket?"

ACM Coffee Break Puzzle Number 22: Missing Dollar
Three friends go to a restaurant and split the bill evenly. The total bill is $30, so each person contributes $10. The waiter realizes there was a mistake and the actual bill was only $25. He gives $5 back to the busboy to return to the friends. The busboy, however, decides to keep $2 for himself and gives $1 back to each friend.
Now, each friend has paid $9 (since they originally paid $10, but got $1 back), totaling $27. The busboy kept $2. That adds up to $29. But the original total was $30. Where is the missing dollar?

ACM Coffee Break Puzzle Number 23: The Well
A man fell in a well. The well is 30 meters deep. In a day, he can clim 4 meters, but he slips down 3 meters. How many days would it take for him to come out of the well?

ACM Coffee Break Puzzle Number 24: Batteries
You have eight batteries, but only four of them work. You have to use them for a flashlight, which needs two working batteries. What is the minimum number of battery pairs you need to test to ensure that the flashlight is turned on?

ACM Coffee Break Puzzle Number 25: Beach Towels
Three friends lay their identical beach towels out flat on the sand side by side in a row. Then, a big gust of wind flips one towel completely over, folds the second in half, and flips the third upside down and over. Which towel is still lying in the original position relative to the sun?

ACM Coffee Break Puzzle Number 26: The Pearl
You're at the beach and find 5 identical seashells in a row: A, B, C, D, and E. One contains a pearl. A wise crab knows where the pearl is, will answer two yes/no questions, and may lie once.
You ask: "Is the pearl under A, B, or C?" "Is the pearl under A, D, or E?" Both answers are yes. Can you guarantee where the pearl is?
